|
1.
Цель работы
Изучить машину
Тьюринга и способы написания алгоритмов для нее. Получить навыки по написанию
алгоритмов решения различных задача для машины Тьюринга.
2.
Теоретический материал
Машина Тьюринга (МТ)
состоит из счетной ленты, читающей и пишущей головки, лентопротяжного механизма
и операционного исполнительного устройства, которое может находиться в одном из
дискретных состояний q0,
q1,
..., qs,
принадлежащих некоторой конечной совокупности (алфавиту внутренних состояний).
При этом q0
называется начальным состоянием.
Читающая и пишущая головка
может читать буквы рабочего алфавита А = {а0, a1,
..., аt},
стирать их и печатать. Каждая ячейка ленты в каждый момент времени занята буквой
из множества А. Чаще всего встречается буква а0 -
«пробел».
Головка находится в каждый
момент времени над некоторой ячейкой ленты - текущей рабочей ячейкой.
Лентопротяжный механизм может перемещать ленту так, что головка оказывается над
соседней ячейкой ленты. При этом возможна ситуация выхода за левый край ленты
(ЛК), которая является аварийной, или машинного останова (МО), когда
машина выполняет предписание об остановке.
Порядок работы МТ (с рабочим
алфавитом а0, a1, ..., аt
и состояниями q0,
q1,
..., qs)
описывается таблицей машины Тьюринга.
Эта таблица является матрицей с четырьмя столбцами и (s
+ 1) (t + 1) строками.
Каждая строка имеет вид
qiajvijqij,
0≤i≤s,
0≤j≤t,
qij
принадлежит
{q0,q1,
… qs}
где:
-
qi
начальное состояние;
-
aj
обозначен элемент алфавита {а0, a1, ...,
аt};
-
vij
– действие МТ, состоящее либо в занесении в ячейку ленты символа алфавита а0,
a1, ..., аt,
либо множества предписаний для лентопротяжного механизма: l – переместить
ленту влево, r –переместить ленту вправо, s – остановить машину;
-
qij
является
последующим состоянием.
МТ работает согласно следующим
правилам:
-
если МТ находится
в состоянии
qi,
головка
прочитывает символ в рабочей ячейке.
-
Если vij
– буква рабочего алфавита, то головка стирает содержимое рабочей ячейки и
заносит туда эту букву.
-
Если vij
– команда r или l для лентопротяжного механизма, то лента
сдвигается на одну ячейку вправо или влево (если не происходит выход за левый
край ленты) соответственно.
-
Если vij
=s,
то происходит машинный останов.
Пример №1.
Алгоритм прибавления единицы к числу п в десятичной системе счисления.
Дана десятичная запись числа п, требуется получить десятичную запись
числа п + 1.
Внешний алфавит МТ должен
состоять из десяти цифр 0,1,2,3,4,5,6,7,8,9 и символа пробела _. Эти цифры
записывают по одной в ячейке (подряд, без пропусков).
При этом
достаточно иметь два внутренних состояния машины: q1 и q2.
Предположим, что в начальный
момент головка находится над одной из цифр числа, а машина находится в состоянии
q1. Тогда задача может быть решена в два этапа:
движения головки к цифре единиц числа (во внутреннем состоянии q1)
и замене этой цифры на единицу большую (с учетом переноса 1 в следующий разряд,
если это 9), во внутреннем состоянии q2.
|
аi |
qi |
|
q1 |
q2 |
|
0
|
0Пq1 |
1Cq2 |
|
1
|
1Пq1 |
2Cq2 |
|
2
|
2Пq1 |
3Cq2 |
|
3
|
3Пq1 |
4Cq2 |
|
4
|
4Пq1 |
5Cq2 |
|
5
|
5Пq1 |
6Cq2 |
|
6
|
6Пq1 |
7Cq2 |
|
7
|
7Пq1 |
8Cq2 |
|
8
|
8Пq1 |
9Cq2 |
|
9
|
9Пq1 |
0Лq2 |
|
-
|
-Лq2 |
1Cq2 |
Пример №2.
На ленте машины Тьюринга содержится последовательность символов “+”. Напишите
программу для машины Тьюринга, которая каждый второй символ “+” заменит на “–”.
Замена начинается с правого конца последовательности. Автомат в состоянии q1
обозревает один из символов указанной последовательности.
Решение.
В состоянии q1
машина ищет правый конец числа.
В состоянии q2
– пропускает знак “+”, при достижении конца последовательности –
останавливается.
В состоянии q3 машина
знак “+” заменяет на знак “–”, при достижении конца последовательности она
останавливается.
|
|
a0
|
+
|
-
|
|
q1
|
a0Лq2
|
+Пq1
|
|
|
q2
|
a0Cq2
|
+Лq3
|
|
|
q3
|
a0Cq2
|
-Лq2
|
|
Пример №3.
Дана десятичная запись натурального числа n > 1. Разработать машину
Тьюринга, которая уменьшала бы заданное число n на 1. Автомат в состоянии
q1 обозревает правую цифру числа.
Решение
Состояние q1
– уменьшаем младшую (очередную) цифру на 1. Если она не равна нулю, то после
уменьшения сразу – останов, если же младшая цифра равна 0, то вместо нее пишем
9, смещаемся влево и вновь выполняем вычитание.
В клетку [a0,
q1] машина Тьюринга никогда не попадет, поэтому ее можно не
заполнять.

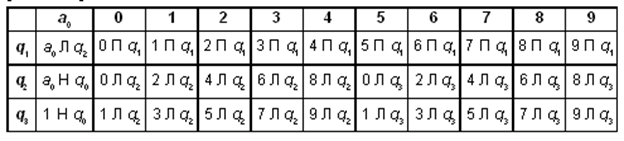
Пример №4.
На ленте машины Тьюринга находится число, записанное в десятичной системе
счисления. Умножить это число на 2. Автомат в состоянии q1
обозревает крайнюю левую цифру числа.
Решение
Состояние q1 — поиск
правой (младшей) цифры числа.
Состояние q2 — умножение
очередной цифры числа на 2 без прибавления 1 переноса.
Состояние q3 — умножение
очередной цифры числа на 2 с прибавлением 1 переноса.
3.
Порядок выполнения работы
1.
Изучить предлагаемый теоретический
материал.
2.
Выполнить следующие
задания:
1.
Заменить во входном слове из 0 и 1 все
буквы 0 на 1 и наоборот.
2.
Дана десятичная запись натурального числа
n > 1. Разработать машину Тьюринга, которая уменьшала бы заданное число
n на 5. Автомат в состоянии q1 обозревает одну из цифр
числа. Кроме самой программы-таблицы, описать словами, что выполняется машиной в
каждом состоянии.
3.
На ленте машины Тьюринга находится число,
записанное в десятичной системе счисления. Умножить это число на 3. Автомат в
состоянии q1 обозревает самую правую цифру числа. Кроме самой
программы-таблицы, описать словами, что выполняется машиной в каждом состоянии.
4.
Удалить из слова его второй символ.
A={a,b}.
5.
Переместить ноль через блок единиц. (011111
->
111110).
6.
Во входном слове из 0 и 1 переместить
первую букву в конец слова.
7.
Удвоение блока из 1.
8.
Обратить слово из 0 и 1 (на выходе буквы
слова в обратном порядке).
4.
Содержание отчета
В отчете следует указать:
-
Цель работы
-
Введение
-
Программно-аппаратные средства, используемые при выполнении работы.
-
Основную часть (описание самой работы), выполненную согласно требованиям к
результатам выполнения лабораторного практикума.
-
Заключение (выводы).
-
Список используемой литературы.
5.
Литература
1.
Могилев А.В., Пак Н.И., Хенкер Е.К.
Информатика. Учебное пособие. – М.: Академия, 2004, 3-е издание.
2.
Могилев А.В., Пак Н.И., Хенкер Е.К.
Практикум по информатике. - М.: Академия, 2005, 2-е изд.
3.
Шауцукова Л.З. Информатика
http://book.kbsu.ru,
2002.
4.
Сырецкий Г.А. Информатика. Фундаментальный курс.
В 2
томах. – БХВ-Петербург,
2007.
5.
Каймин В.А. Информатика. – М.: Инфра-М.
2001, 2-е изд., доп. и перераб.
6.
Острейковский В.А., Полякова И.В.
Информатика. Теория и практика. – М.: Оникс, 2008.
7.
Степанов А.Н. Информатика. Учебник для
вузов. – СПб.: Питер, 2006, 4-е изд.
8.
Рыжиков Ю.И.
Информатика. Лекции и практикум. – СПб.: Корона принт.
2000.
9.
Андреева Е., Фалина И. Информатика. Системы
счисления и компьютерная арифметика. – М.: Лаборатория Базовых Знаний. 1999.
10. Л.З.
Информатика
http://book.kbsu.ru,
2002.
11. В.М.
Введение в информатику http://www.intuit.ru/department/informatics/intinfo,
2006.
12. В.М.
Введение в информатику. Практикум http://www.intuit.ru/department/informatics/intinfopr,
2008.
13. Е.А.
Практическая информатика http://www.intuit.ru/department/se/pinform, 2006
14. Н.Н.
Стили и методы программирования http://www.intuit.ru/department/se/progstyles,
2005
|
