Глава 2. Меры информации  

Семиотика (греч. semeion – знак, признак) – наука, занимающаяся исследованием свойств знаков и знаковых систем.

Семиотика выделяет следующие уровни передачи информации:

-       Синтаксический, рассматриваются внутренние свойства сообщений.

-       Семантический,  анализируется смысловое содержание сообщения, его отношение к источнику информации

-       Прагматический,  рассматривается потребительское содержание сообщения, его отношение к получателю.

Рассмотрим уровни более подробно. Синтаксический уровень рассматривает технические проблемы совершенствования методов передачи сообщений и их материальных носителей – сигналов. Проблемы доставки получателю сообщений. Полностью абстрагируются от смыслового содержания сообщений и их целевого предназначения. Учитывают:

-        Тип носителя.

-        Способ представления информации.

-        Скорость передачи и обработки.

-        Размеры кодов представления информации и т.д.

Семантический уровень рассматривает проблемы, связанные с формализацией и учетом смысла передаваемой информации. Проблемы этого уровня чрезвычайно сложны, так как смысловое содержание информации больше зависит от получателя, чем от семантики сообщения, представленного на каком-либо языке. Учитываются:

-       Анализируется сведенья, которые отражает информация.

-        Выявляется смысл информации.

-        Выявляется содержание информации.

-        Осуществляется обобщение.

Прагматический уровень рассматривает проблемы, связанные с определением ценности и полезности информации для потребителя. Интересуют последствия от получения и использования данной информации потребителем. Учитываются:

-       Ценность информации может быть различной для разных потребителей.

-       Фактор доставки, актуальность доставки и использования.

Исходя из рассмотренных уровней выделяются следующие меры информации синтаксическая, семантическая и прагматическая.

Синтаксическая мера информации

Определить понятие «количество информации» довольно сложно. В решении этой проблемы существуют два основных подхода. Исторически они возникли почти одновременно. В конце 40-х годов XX века один из основоположников кибернетики американский математик Клод Шеннон развил вероятностный подход к измерению количества информации, а работы по созданию ЭВМ привели к «объемному» подходу.

Таким образом, на синтаксическом уровне для измерения информации вводятся два параметра:

-       Объем информации (объемный подход).

-       Количество информации (вероятностный подход).

Объемный подход

Если  количество информации, содержащейся в сообщении из одного символа, принять за единицу, то объем информации (данных) V_Д в любом другом сообщении будет равен количеству  символов (разрядов) в этом сообщении. В памяти компьютера объем информации записывается двоичными знаками и равен количеству требуемых для этой записи двоичных кодов.

Объём данных (V_Д) в техническом смысле этого слова как информационный объём сообщения или как объём памяти, необходимый для хранения сообщения без каких-либо изменений.

Единицы измерения информации – 1 бит (от английского выражения Binary digiTs – двоичные цифры) = количество двоичных цифр (0 и 1). Пример: код 11001011 имеет объем данных V= 8 бит.

Создатели компьютеров отдают предпочтение именно двоичной системе счисления потому, что в техническом устройстве наиболее просто реализовать два противоположных физических состояния: некоторый физический элемент, имеющий два различных состояния: намагниченность в двух противоположных направлениях; прибор, пропускающий или нет электрический ток; конденсатор, заряженный или незаряженный и т.п.

Для удобства использования введены и более крупные, чем бит, единицы количества информации:

-       1 байт = 8 бит.

-       1 Кбайт = 1024 байт = 210 байт.

-       1 Мбайт = 1024 Кбайт  = 220 байт =1 048 576 байт.

-       1 Гбайт = 1024 Мбайт = 230 байт = 1 073 741 824 байт.

-       1 Тбайт = 1024 Гбайт = 240 байт = 1 099 511 627 776 байт.

Вероятностный подход

События, о которых нельзя сказать произойдут они или нет, пока не будет осуществлен эксперимент, называются случайными. Отдельный повтор случайного события называется опытом, а интересующий нас исход этого опыта – благоприятным.

Если N – общее число опытов, а N_А – количество благоприятных исходов случайного события А, то отношение N_A/N, называется относительной частотой появления события А.

В разных сериях  опытов частота может быть различна, но при увеличении количества опытов относительная частота все меньше отклоняется от некоторой константы, ее наличие называется статической устойчивостью частот.

Если все исходы опыта конечны и равновозможные, то их вероятность равна P=1/n, где n – число исходов.

Энтропия (H) – численная мера измеряющая неопределенность.

 H = f(n).

Свойства энтропии:

1.   f(1) = 0, так как при n=1 исход не является случайным и неопределенность отсутствует.

2.  f(n) возрастает с ростом n, чем больше возможных исходов, тем труднее предсказать результат.

3.   Если a и b два независимых опыта с количеством равновероятных исходов n_a и n_b, то мера их суммарной неопределенности равна сумме мер неопределенности каждого из опытов:

     f(n_a) +f(n_b) = f(n_a, n_b).

4.     Количество информации – разность неопределенностей “До” и ”После” опыта: I = H₁ - H₂.

Рассмотрим в качестве примера опыт, связанный с бросанием правильной игральной кости, имеющей N граней (наиболее распространенным является случай шестигранной кости: N = 6). Результаты данного опыта могут быть следующие: выпадение грани с одним из следующих знаков: 1,2,... N.

Если варьировать число граней N и число бросаний кости (обозначим эту величину через М), общее число исходов (векторов длины М, состоящих из знаков 1,2,.... N) будет равно X=N^M, где М – число попыток. Так, в случае двух бросаний кости с шестью гранями имеем: Х = 6² = 36

Ситуацию с бросанием М раз кости можно рассматривать как некую сложную систему, состоящую из независимых друг от друга подсистем – «однократных бросаний кости». Энтропия такой системы в М раз больше, чем энтропия одной системы (так называемый «принцип аддитивности энтропии»).

Энтропия системы из М бросаний кости будет в M раз больше, чем энтропия системы однократного бросания кости – принцип аддитивности энтропии.

f(N^M) = M · f(N)

ln X = M · ln N

M = (ln X) /  (ln N)

Подставляем полученное для M значение в первоначальную формулу:

f (X) = (ln X)· f (N)/  (ln N) 

Обозначим через K = f (N)/  (ln N). Получим f (X) = K · ln X или  H = K · ln X. Обычно принимают K = 1/ ln 2. Таким образом, получим формулу Хартли для равновозможных исходов:

H = ln₂ N.

Все N исходов рассмотренного выше опыта являются равновероятными и поэтому можно считать, что на «долю» каждого исхода приходится одна N-я часть общей неопределенности опыта. При этом вероятность i-го исхода Р_i равняется, очевидно, 1/N. Таким образом, формула Шеннона для неравновозможных исходов выглядит следующим образом:

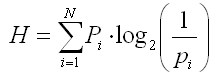
Информация – это содержание сообщения, понижающего неопределенность некоторого опыта с неоднозначным исходом;  убыль связанной с ним энтропии является количественной мерой информации.

Важным при введении какой-либо величины является вопрос о том, что принимать за единицу ее измерения. Очевидно, Н будет равно единице при N = 2. Иначе говоря, в качестве единицы принимается количество информации, связанное с проведением опыта, состоящего в получении одного из двух равновероятных исходов (примером такого опыта может служить бросание монеты при котором возможны два исхода: «орел», «решка»). Такая единица количества информации называется «бит».

Количество информации (в битах), заключенное в двоичном слове, равно числу двоичных знаков в нем.

H = ln₂ 2 = 1 бит.

Семантическая мера информации

Тезаурус – это совокупность сведений, которыми располагает пользователь или система.

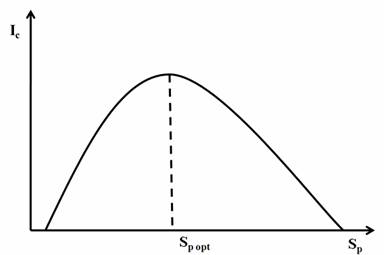
Рисунок 10 - Зависимость количества семантической информации, воспринимаемой потребителем, от его тезауруса.

где S_p – тезаурус пользователя, I_c – семантическая мера информации.

При Sp → 0 пользователь не воспринимает, не понимает поступающую информацию;

При Sp → ∞ пользователь все знает, и поступающая информация ему не нужна.

Относительной мерой количества семантической информации может служить коэффициент содержательности С, который определяется как отношение количества семантической информации к ее объему.

C = I / V_Д

Прагматическая мера информации

Эта мера определяет полезность информации (ценность) для достижения пользователем поставленной цели. Эта мера также величина относительная, обусловленная особенностями использования этой информации в той или иной системе.

Ценность информации целесообразно измерять в тех же самых единицах (или близких к ним), в которых измеряется целевая функция.

Целевая функция – есть математическое выражение некоторого критерия качества одного объекта (решения, процесса и т.д.) в сравнении с другим.

Сопоставление мер информации