|
1.
Цель работы
Изучить понятие
алгоритма, его свойства и способы представления. Получить навыки по построению
алгоритмов для решения задача в виде блок-схем и псевдокода.
2.
Теоретический материал
Блок-схемы
Графическое
описание алгоритма, называется блок-схемой. Блок-схема – это
ориентированный граф, указывающий порядок исполнения команд алгоритма. Вершины
графа могут быть одного из трех типов:
-
функциональная
(имеющая один вход и один выход);
-
предикатная
(имеющая один вход и два выхода);
-
объединяющая
(обеспечивающая передачу управления от одного из двух входов к выходу).
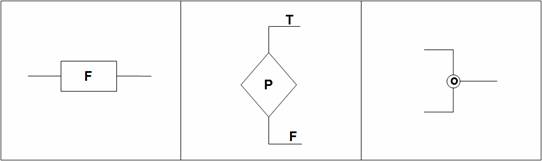
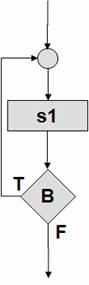
Примеры блок-схем, имеющих
особое значение для практики алгоритмизации.
|
 |
 |
 |
 |
|
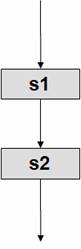
Композиция,
Следование |
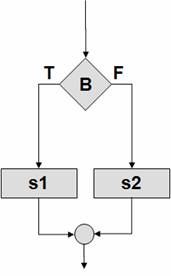
Альтернатива,
Развилка |
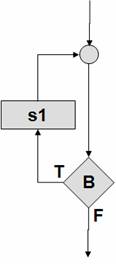
Цикл
с предусловием |
Цикл
с постусловием |
|
 |
 |
|
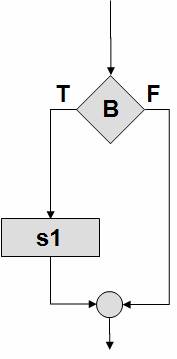
Неполная
развилка |
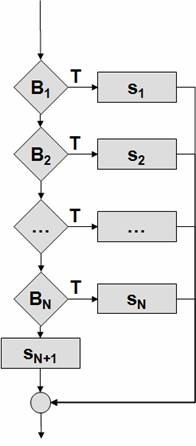
Структура
“выбор” |
Дополнительные блоки блок-схемы
|
 |
Начало (конец)
алгоритма
|
|
 |
Выполнение
операций, изменяющих команды
|
|
 |
Вызов
вспомогательного алгоритма
|
|
 |
Ввод-вывод данных
|
Алгоритм должен быть составлен
таким образом, чтобы исполнитель, в расчете на которого он создан, мог
однозначно и точно следовать командам алгоритма и эффективно получать
определенный результат.
Свойства алгоритмов:
1.
Описываемый процесс должен быть разбит на
последовательность отдельных шагов. Возникающая в результате такого разбиения
запись представляет собой упорядоченную совокупность четко разделенных друг от
друга предписаний, образующих прерывную структуру алгоритма. Рассмотренное
свойство алгоритмов называют дискретностью.
2.
Используемые на практике алгоритмы
составляются с ориентацией на определенного исполнителя. Чтобы составить для
него алгоритм, нужно знать, какие команды этот исполнитель может понять и
исполнить, а какие – не может. У каждого исполнителя имеется своя
система команд. Составляя запись алгоритма для определенного исполнителя, можно
использовать лишь те команды, которые имеются в его СКИ. Это свойство алгоритмов
будем называть понятностью.
3.
Будучи понятным, алгоритм не должен
содержать предписаний, смысл которых может восприниматься неоднозначно, т.е.
одна и та же команда, будучи понятна разным исполнителям, после исполнения
каждым из них должна давать одинаковый результат. Запись алгоритма должна быть
настолько четкой, полной и продуманной в деталях, чтобы у исполнителя не могло
возникнуть потребности в принятии решений, не предусмотренных составителем
алгоритма. Кроме того, в алгоритмах недопустимы также ситуации, когда после
выполнения очередной команды алгоритма исполнителю неясно, какая из команд
алгоритма должна выполняться на следующем шаге. Отмеченное свойства алгоритмов
называют определенностью или детерминированностью.
4.
Обязательное требование к алгоритмам - результативность. Смысл этого требования состоит в том, что при точном
исполнении всех предписаний алгоритма процесс должен прекратиться за конечное
число шагов и при этом должен получиться определенный результат. Вывод о том,
что решения не существует - тоже результат.
5.
Наиболее распространены алгоритмы,
обеспечивающие решение не одной конкретной задачи, а некоторого класса задач
данного типа. Это свойство алгоритма называют массовостью. В простейшем
случае массовость обеспечивает возможность использования различных исходных
данных.
Алгоритмический язык
(псевдокод)
Псевдокод
представляет собой систему обозначений и правил, предназначенную для
единообразной записи алгоритмов.
Псевдокод занимает
промежуточное место между естественным и формальным языками. С одной стороны, он
близок к обычному естественному языку, поэтому алгоритмы могут на нем
записываться и читаться как обычный текст. С другой стороны, в псевдокоде
используются некоторые формальные конструкции и математическая символика, что
приближает запись алгоритма к общепринятой математической записи.
В псевдокоде не приняты строгие
синтаксические правила для записи команд, присущие формальным языкам, что
облегчает запись алгоритма на стадии его проектирования и дает возможность
использовать более широкий набор команд, рассчитанный на абстрактного
исполнителя.
Однако в псевдокоде обычно
имеются некоторые конструкции, присущие формальным языкам, что облегчает переход
от записи на псевдокоде к записи алгоритма на формальном языке. В частности, в
псевдокоде, так же, как и в формальных языках, есть служебные слова, смысл
которых определен раз и навсегда. Они выделяются в печатном тексте жирным
шрифтом, а в рукописном тексте подчеркиваются.
Единого или формального
определения псевдокода не существует, поэтому возможны различные псевдокоды,
отличающиеся набором служебных слов и основных (базовых) конструкций.
Примером
псевдокода является школьный алгоритмический язык в русской нотации (школьный
АЯ), описанный в учебнике А.Г.
Кушниренко и др. "Основы информатики и вычислительной техники", 1991. Этот язык
в дальнейшем мы будем называть просто "алгоритмический язык".
Основные служебные слова
|
алг
(алгоритм) |
сим
(символьный) |
дано |
для |
да |
|
арг
(аргумент) |
лит
(литерный) |
надо |
от |
нет |
|
рез
(результат) |
лог
(логический) |
если |
до |
при |
|
нач
(начало) |
таб(таблица) |
то |
знач
|
выбор |
|
кон
(конец) |
нц
(начало цикла) |
иначе |
и |
ввод |
|
цел
(целый) |
кц
(конец цикла) |
все |
или |
вывод |
|
вещ
(вещественный) |
длин
(длина) |
пока
|
не |
утв |
Общий вид алгоритма:
алг
название алгоритма (аргументы и результаты)
дано условия
применимости алгоритма
надо цель выполнения
алгоритма
нач описание
промежуточных величин
| последовательность команд
(тело алгоритма)
кон
Часть алгоритма от слова алг
до слова нач
называется заголовком, а часть, заключенная между словами нач и
кон - телом алгоритма.
В предложении алг после
названия алгоритма в круглых скобках указываются характеристики (арг,
рез) и тип значения (цел, вещ, сим, лит или лог) всех
входных (аргументы) и выходных (результаты) переменных. При описании
массивов (таблиц) используется служебное слово таб, дополненное
граничными парами по каждому индексу элементов массива.
Примеры предложений алг:
алг
Объем и площадь цилиндра ( арг вещ R, H, рез вещ V, S )
алг
Корни КвУр ( арг вещ а, b, c, рез вещ x1, x2, рез лит t )
алг
Исключить элемент ( арг цел N, арг рез вещ таб А[1:N] )
алг
Диагональ ( арг цел N, арг цел таб A[1:N, 1:N], рез лит
Otvet )
Предложения дано и
надо не обязательны. В них рекомендуется записывать утверждения, описывающие
состояние среды исполнителя алгоритма, например:
1. алг Замена (арг лит Str1, Str2, арг рез лит Text)
дано | длины подстрок Str1 и Str2 совпадают
надо | всюду в строке Text подстрока Str1 заменена на Str2
2. алг Число максимумов (арг цел N, арг вещ таб A[1:N], рез цел K)
дано | N>0
надо | К — число максимальных элементов в таблице А
3. алг Сопротивление (арг вещ R1, R2, арг цел N, рез вещ R)
дано | N>5, R1>0, R2>0
надо | R — сопротивление схемы
Здесь в предложениях дано
и надо после знака "|" записаны комментарии. Комментарии можно
помещать в конце любой строки. Они не обрабатываются транслятором, но
существенно облегчают понимание алгоритма.
Команда
присваивания. Служит
для вычисления выражений и присваивания их значений переменным. Общий вид: А
:= В, где знак ":=" означает команду заменить прежнее значение
переменной, стоящей в левой части, на вычисленное значение выражения,
стоящего в правой части.
Например,
a := (b+c) * sin(Pi/4);
i := i+1.
Команды ввода
и вывода.
-
ввод
имена переменных
-
вывод
имена переменных, выражения, тексты.
Команды если
и выбор. Применяют для организации
ветвлений.
Команды для
и пока. Применяют для организации циклов.
Пример записи
алгоритма на школьном АЯ
алг Сумма квадратов (арг цел n, рез цел S)
дано | n > 0
надо | S = 1*1 + 2*2 + 3*3 + ... + n*n
нач цел i
ввод n; S:=0
нц для i от 1 до n
S:=S+i*i
кц
вывод "S = ", S
кон
Итерационные циклы
Особенностью итерационного
цикла является то, что число повторений операторов тела цикла заранее
неизвестно. Для его организации используется цикл типа пока. Выход из
итерационного цикла осуществляется в случае выполнения заданного условия.
На каждом шаге вычислений
происходит последовательное приближение к искомому результату и проверка условия
достижения последнего.
Пример. Составить алгоритм
вычисления бесконечной суммы
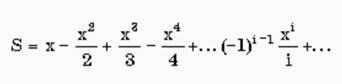
с заданной точностью
e
(для данной знакочередующейся бесконечной суммы требуемая точность будет
достигнута, когда очередное слагаемое станет по абсолютной величине меньше
e).
Вычисление сумм — типичная
циклическая задача. Особенностью же нашей конкретной задачи является то, что
число слагаемых (а, следовательно, и число повторений тела цикла) заранее
неизвестно. Поэтому выполнение цикла должно завершиться в момент достижения
требуемой точности.
При составлении алгоритма нужно
учесть, что знаки слагаемых чередуются и степень числа х в числителях
слагаемых возрастает.
Решая эту задачу "в лоб" путем
вычисления на каждом i-ом шаге частичной суммы
S:=S + ((-1)**(i-1)) * (x**i) /
i ,
мы получим очень неэффективный
алгоритм, требующий выполнения большого числа операций. Гораздо лучше
организовать вычисления следующим образом: если обозначить числитель какого-либо
слагаемого буквой р , то у следующего слагаемого числитель будет равен —р*х
(знак минус обеспечивает чередование знаков слагаемых), а само слагаемое m
будет равно p/i , где i — номер слагаемого.
Алгоритм
алг Сумма (арг вещ x, Eps, рез вещ S)
надо | S = x - x**2/2 + x**3/3 - ...
S := 0; i := 1 | начальные значения
p := -p*x | p - числитель очередного слагаемого
m := p/i | m - очередное слагаемое
S := S + m | S - частичная сумма
Алгоритм, в состав которого
входит итерационный цикл, называется итеpационным алгоpитмом.
Итерационные алгоритмы используются при реализации итерационных численных
методов.
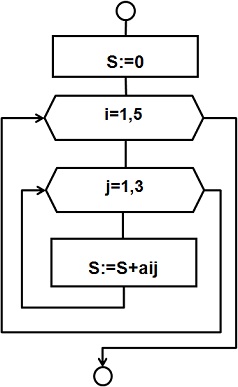
Пример вложенных циклов
“для”
Вычислить сумму элементов
заданной матрицы А(5,3).
Пример вложенных циклов
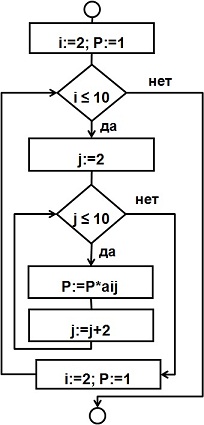
“пока”
Вычислить произведение тех
элементов заданной матрицы A(10,10), которые расположены на пересечении четных
строк и четных столбцов.
3.
Порядок выполнения работы
1.
Изучить предлагаемый теоретический
материал.
2.
Выполнить следующие
задания:
1.
Определите
значение целочисленной переменной S после выполнения операторов:
a)
S:=128
b)
S:=1; a:=1
c)
S:=1; a:=1
d)
S:=0
e)
нц для i от 1 до 3
f)
нц для i от 1 до 2
2.
Составьте алгоритм
решения задач разветвляющейся структуры и в виде блок-схем и в виде псевдокода:
a)
определить,
является ли треугольник с заданными сторонами a, b, c равнобедренным;
b)
определить
количество положительных чисел среди заданных чисел a, b и c;
c)
меньшее из двух
заданных неравных чисел увеличить вдвое, а большее оставить без изменения;
d)
числа a и b —
катеты одного прямоугольного треугольника, а c и d — другого; определить,
являются ли эти треугольники подобными;
e)
даны три точки на
плоскости; определить, какая из них ближе к началу координат;
f)
определить,
принадлежит ли заданная точка (x, y) плоской фигуре, являющейся кольцом с
центром в начале координат, с внутренним радиусом r1 и внешним радиусом r2 ;
g)
упорядочить по
возрастанию последовательность трех чисел a, b и c.
4.
Содержание отчета
В отчете следует указать:
-
Цель работы
-
Введение
-
Программно-аппаратные средства, используемые при выполнении работы.
-
Основную часть (описание самой работы), выполненную согласно требованиям к
результатам выполнения лабораторного практикума.
-
Заключение (выводы).
-
Список используемой литературы.
5.
Литература
1.
Могилев А.В., Пак Н.И., Хенкер Е.К.
Информатика. Учебное пособие. – М.: Академия, 2004, 3-е издание.
2.
Могилев А.В., Пак Н.И., Хенкер Е.К.
Практикум по информатике. - М.: Академия, 2005, 2-е изд.
3.
Шауцукова Л.З. Информатика
http://book.kbsu.ru,
2002.
4.
Сырецкий Г.А. Информатика. Фундаментальный курс.
В 2
томах. – БХВ-Петербург,
2007.
5.
Каймин В.А. Информатика. – М.: Инфра-М.
2001, 2-е изд., доп. и перераб.
6.
Острейковский В.А., Полякова И.В.
Информатика. Теория и практика. – М.: Оникс, 2008.
7.
Степанов А.Н. Информатика. Учебник для
вузов. – СПб.: Питер, 2006, 4-е изд.
8.
Рыжиков Ю.И.
Информатика. Лекции и практикум. – СПб.: Корона принт.
2000.
9.
Андреева Е., Фалина И. Информатика. Системы
счисления и компьютерная арифметика. – М.: Лаборатория Базовых Знаний. 1999.
10. Л.З.
Информатика
http://book.kbsu.ru,
2002.
11. В.М.
Введение в информатику http://www.intuit.ru/department/informatics/intinfo,
2006.
12. В.М.
Введение в информатику. Практикум http://www.intuit.ru/department/informatics/intinfopr,
2008.
13. Е.А.
Практическая информатика http://www.intuit.ru/department/se/pinform, 2006
14. Н.Н.
Стили и методы программирования http://www.intuit.ru/department/se/progstyles,
2005
|
