Понятие алгоритма – одно
из фундаментальных понятий информатики. Алгоритмизация наряду с моделированием
выступает в качестве общего метода информатики.
К реализации определенных
алгоритмов сводятся процессы управления в различных системах, что делает понятие
алгоритма близким и кибернетике.
Алгоритмы являются объектом
систематического исследования пограничной между математикой и информатикой
научной дисциплины, примыкающей к математической логике – теории алгоритмов.
Само слово «алгоритм»
происходит от
algorithmi
– латинской формы написания имени великого математика IX века аль-Хорезми,
который сформулировал правила выполнения арифметических действий.
Первоначально под алгоритмами
понимали только правила выполнения четырех арифметических действий над
многозначными числами.
Определение алгоритма:
1.
Последовательность действий (операций) и
правил их выполнения или команд, предназначенных для решения определенной задачи
или группы задач;
2.
Предписание, определяющее ход
вычислительного процесса, связанного с преобразованием данных от некоторого их
исходного состояния к требуемому результату.
Формальные описания алгоритмов
аналогичны представлениям основных частей программ, которые их реализуют,
поэтому многое, что относят к описанию конкретных программ, применимо к
алгоритму и наоборот.
Понятие исполнителя
невозможно определить с помощью какой-либо формализации. Исполнителем может быть
человек, группа людей, робот, станок, компьютер, язык программирования и т.д.
Важнейшим свойством,
характеризующим любого из этих исполнителей, является то, что исполнитель умеет
выполнять некоторые команды. Вся совокупность команд, которые данный исполнитель
умеет выполнять, называется системой команд исполнителя (СКИ).
Исполнитель не вникает в смысл
того, что он делает, но получает необходимый результат. В таком случае говорят,
что исполнитель действует формально, т. е. отвлекается от содержания
поставленной задачи и только строго выполняет некоторые правила, инструкции.
Наличие алгоритма формализует
процесс решения задачи, исключает рассуждение исполнителя.
Введение в рассмотрение понятия
“исполнитель” позволяет определить алгоритм как понятное и точное предписание
исполнителю совершить последовательность действий, направленных на достижение
поставленной цели.
Алгоритм, составленный для
некоторого исполнителя, можно представить различными способами:
-
с помощью
графического описания;
-
с помощью
словесного описания;
-
в виде таблицы;
-
в виде
последовательностью формул.
Графическое описание алгоритма,
называется блок-схемой. Блок-схема – это ориентированный граф,
указывающий порядок исполнения команд алгоритма.
Вершины графа могут быть одного
из трех типов:
-
функциональная
(имеющая один вход и один выход);
-
предикатная
(имеющая один вход и два выхода);
-
объединяющая
(обеспечивающая передачу управления от одного из двух входов к выходу).
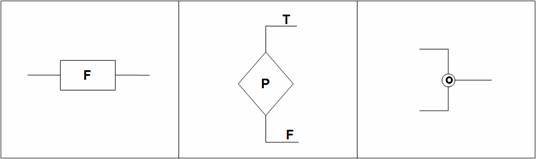
Рисунок 31 – Блок-схема
Из данных элементарных блоков
можно построить четыре блок-схемы, имеющие особое значение для практики
алгоритмизации.
|
 |
 |
 |
 |
|
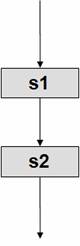
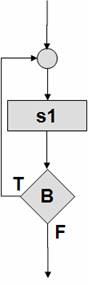
Рисунок 32 –
Композиция, cледование |
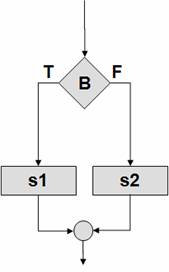
Рисунок 33 –
Альтернатива, hазвилка |
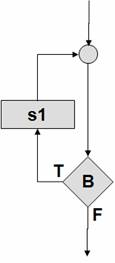
Рисунок 34 –
Цикл с предусловием |
Рисунок 35 –
Цикл с постусловием |
|
 |
 |
|
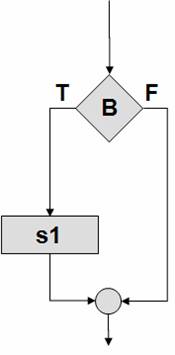
Рисунок 36 –
Неполная развилка
|
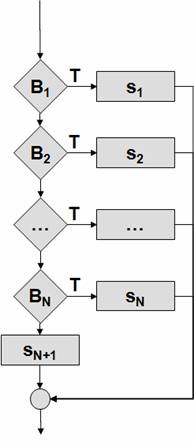
Рисунок 37 –
Структура
“выбор” |
Дополнительные блоки блок-схемы
|
 |
Начало (конец)
алгоритма
|
|
 |
Выполнение
операций, изменяющих команды
|
|
 |
Вызов
вспомогательного алгоритма
|
|
 |
Ввод-вывод данных
|
Алгоритм должен быть составлен
таким образом, чтобы исполнитель, в расчете на которого он создан, мог
однозначно и точно следовать командам алгоритма и эффективно получать
определенный результат.
Свойства алгоритмов:
1.
Описываемый процесс должен быть разбит на
последовательность отдельных шагов. Возникающая в результате такого разбиения
запись представляет собой упорядоченную совокупность четко разделенных друг от
друга предписаний, образующих прерывную структуру алгоритма. Только выполнив
требования одного предписания, можно приступить к выполнению следующего.
Дискретная структура алгоритмической записи может, например, подчеркиваться
сквозной нумерацией отдельных команд алгоритма, хотя это требование не является
обязательным. Рассмотренное свойство алгоритмов называют дискретностью.
2.
Используемые на практике алгоритмы
составляются с ориентацией на определенного исполнителя. Чтобы составить для
него алгоритм, нужно знать, какие команды этот исполнитель может понять и
исполнить, а какие – не может. У каждого исполнителя имеется своя
система команд. Составляя запись алгоритма для определенного исполнителя, можно
использовать лишь те команды, которые имеются в его СКИ. Это свойство алгоритмов
будем называть понятностью.
3.
Будучи понятным, алгоритм не должен
содержать предписаний, смысл которых может восприниматься неоднозначно, т.е.
одна и та же команда, будучи понятна разным исполнителям, после исполнения
каждым из них должна давать одинаковый результат. Запись алгоритма должна быть
настолько четкой, полной и продуманной в деталях, чтобы у исполнителя не могло
возникнуть потребности в принятии решений, не предусмотренных составителем
алгоритма. Кроме того, в алгоритмах недопустимы также ситуации, когда после
выполнения очередной команды алгоритма исполнителю неясно, какая из команд
алгоритма должна выполняться на следующем шаге. Отмеченное свойства алгоритмов
называют определенностью или детерминированностью.
4.
Обязательное требование к алгоритмам - результативность. Смысл этого требования состоит в том, что при точном
исполнении всех предписаний алгоритма процесс должен прекратиться за конечное
число шагов и при этом должен получиться определенный результат. Вывод о том,
что решения не существует - тоже результат.
5.
Наиболее распространены алгоритмы,
обеспечивающие решение не одной конкретной задачи, а некоторого класса задач
данного типа. Это свойство алгоритма называют массовостью. В простейшем
случае массовость обеспечивает возможность использования различных исходных
данных.
Алгоритмический язык
Достаточно распространенным
способом представления алгоритма является его запись на алгоритмическом
языке, представляющем в общем случае систему обозначений и правил для
единообразной и точной записи алгоритмов и исполнения их.
Между понятиями
“алгоритмический язык” и “языки программирования” есть различие; прежде всего,
под исполнителем в алгоритмическом языке может подразумеваться не только
компьютер, но и устройство для работы “в обстановке”.
Программа, записанная на
алгоритмическом языке, не обязательно предназначена компьютеру.
Практическая же реализация
алгоритмического языка – отдельный вопрос в каждом конкретном случае.
Как и каждый язык,
алгоритмический язык имеет свой словарь. Основу этого словаря составляют слова,
употребляемые для записи команд, входящих в систему команд исполнителя того или
иного алгоритма. Такие команды называют простыми командами.
В алгоритмическом языке
используют слова, смысл и способ употребления которых задан раз и навсегда. Эти
слова называют служебными. Использование служебных слов делает запись
алгоритма более наглядной, а форму представления различных алгоритмов –
единообразной.
Алгоритм, записанный на
алгоритмическом языке, должен иметь название. Название желательно выбирать так,
чтобы было ясно, решение какой задачи описывает данный алгоритм.
Для выделения названия
алгоритма перед ним записывают служебное слово АЛГ (АЛГоритм).
Для указания начала и конца
алгоритма его команды заключают в пару служебных слов НАЧ (НАЧало) и КОН (КОНец).
Команды записывают последовательно.
АЛГ название алгоритма
НАЧ
серия команд алгоритма
КОН
Например,
алгоритм, определяющий движение исполнителя-робота.
АЛГ в_склад
НАЧ
вперед
поворот на 90°
направо
вперед
КОН
При построении новых алгоритмов
могут использоваться алгоритмы, составленные ранее.
Алгоритмы, целиком используемые
в составе других алгоритмов, называют вспомогательными алгоритмами.
Вспомогательным может оказаться
любой алгоритм из числа ранее составленных.
Очень часто при составлении
алгоритмов возникает необходимость использования в качестве вспомогательного
одного и того же алгоритма, который к тому же может быть весьма сложным и
громоздким.
Было бы нерационально, начиная
работу, каждый раз заново составлять и запоминать такой алгоритм для его
последующего использования. Поэтому в практике широко используют, так
называемые, встроенные (или стандартные) вспомогательные алгоритмы, т.е. такие
алгоритмы, которые постоянно имеются в распоряжении исполнителя.
Обращение к таким алгоритмам
осуществляется так же, как и к “обычным” вспомогательным алгоритмам.
Алгоритм может содержать
обращение к самому себе как вспомогательному и в этом случае его называют
рекурсивным.
Если команда обращения
алгоритма к самому себе находится в самом алгоритме, то такую рекурсию называют
прямой.
Возможны случаи, когда
рекурсивный вызов данного алгоритма происходит из вспомогательного алгоритма, к
которому в данном алгоритме имеется обращение. Такая рекурсия называется
косвенной.
АЛГ движение
НАЧ
вперед
вперед
вправо
движение
КОН
Алгоритмы, при исполнении
которых порядок следования команд определяется в зависимости от результатов
проверки некоторых условий, называют разветвляющимися. Для их описания в
алгоритмическом языке используют специальную составную команду – команда
ветвления. Она соответствует блок-схеме “альтернатива” и также может иметь
полную или сокращенную форму.
ЕСЛИ условие ЕСЛИ
условие
ТО серия 1 ТО
серия
ИНАЧЕ серия2
ВСЕ
ВСЕ
Запись на алгоритмическом языке
команды выбора, являющейся развитием команды ветвления:
ВЫБОР
ПРИ условие 1:
серия 1
ПРИ условие 2:
серия 2
…
ПРИ условие
N:
серия N
ИНАЧЕ
серия N+1
ВСЕ
Алгоритмы, при исполнении
которых отдельные команды или серии команд выполняются неоднократно, называют
циклическими. Для организации циклических алгоритмов в алгоритмическом языке
используют специальную составную команду цикла. Она соответствует блок-схемам
типа «итерация» и может принимать следующий вид:
ПОКА
условие НЦ
НЦ
серия
Серия ДО условие
КЦ
КЦ
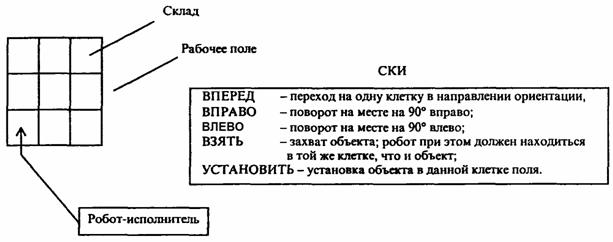
Рисунок 38 – Пример (работа
робота)
|
АЛГ перенос
НАЧ
в_угол3
ЕСЛИ есть
ТО
взять
в_угол3
установить
перенос
ИНАЧЕ
в_угол3
ВСЕ
КОН |
АЛГ в_угол3
НАЧ
до_края
вправо
до_края
вправо
КОН |
АЛГ до_края
НАЧ
ПОКА не_край
НЦ
вперед
КЦ
КОН
|
Жадный алгоритм
Жадный алгоритм —
алгоритм, заключающийся в принятии локально оптимальных решений на каждом этапе,
допуская что конечное решение также окажется оптимальным.
Общего критерия оценки
применимости жадного алгоритма для решения конкретной задачи не существует,
однако, для задач, решаемых жадными алгоритмами характерны две особенности:
-
к ним применим
Принцип жадного выбора (последовательность локально оптимальных выборов даёт
глобально оптимальное решение).
-
они обладают
свойством Оптимальности для подзадач (оптимальное решение задачи содержит
в себе оптимальные решения для всех её подзадач).
Пример. Размен монет.
Задача. Монетная
система некоторого государства состоит из монет достоинством a1
= 1 < a2 < ... < an. Требуется выдать сумму
S наименьшим возможным количеством монет.
Жадный алгоритм решения этой
задачи таков. Берётся наибольшее возможное количество монет достоинства an:
xn=[S/an].
Таким же образом получаем, сколько нужно монет меньшего номинала, и т. д.
Для данной задачи жадный
алгоритм не всегда даёт оптимальное решение. Например, сумму в 10 копеек
монетами в 1, 5 и 6 коп. жадный алгоритм разменивает так: 6 коп. – 1 шт., 1
коп. – 4 шт., в то время как правильное решение – 2 монеты по 5 копеек.
Тем не менее, на всех
реальных монетных системах жадный алгоритм даёт правильный ответ.
|
