|
1.
Цель работы
Изучить системы
счисления и формы представления чисел. Получить навыки по работе с различными
системами счисления, по переводу из одной системы счисления в другую,
а также по представлению числе в нормализованном виде.
2.
Теоретический материал
Система счисления – это способ
наименования и изображения чисел с помощью цифр, то есть символов, имеющих
определенные количественные значения.
В позиционной системе счисления
количественное значение каждой цифры зависит от ее места (позиции) в числе.
Основанием системы счисления называется количество различных цифр, используемых
для изображения числа в позиционной системе счисления. Позицией называется место
каждой цифры в числе.
Перевод целых чисел из одной
системы счисления в другую в общем случае осуществляется по следующим правилам.
Правило 1.
Перевод числа x из системы счисления основанием P в систему счисления с
основанием Q заключается в последовательном нахождении остатков от деления числа
x на основание Q, при этом процесс продолжается до тех пор, пока частное от
деления не будет меньше основания Q. Все вычисления выполняются в системе
счисления с основанием P, т.е. основание Q должно также быть выражено в системе
счисления с основанием P.
Остатки от деления должны быть
выражены цифрами системы счисления с основанием
Q.
Представление искомого числа в системе счисления с основанием
Q
получается выписыванием последнего частного и остатков от деления в обратном
порядке.
Правило 2.
Перевод числа x из системы
счисления основанием P в систему счисления с основанием Q осуществляется путем
представления числа х по степеням основания P. Все вычисления выполняются в
системе счисления с основанием Q, т. е. основание P и цифры исходного числа
должны также быть выражены в системе счисления с основанием Q.
На практике такой порядок
перевода чисел используется при переводе десятичную систему счисления.
23Е16 = ?10
= 2*162+3*161+ Е*160 = 57410
10788 = 1*83+0*82+7*81+6*80
= 57410
Правило 3.
Перевод чисел из восьмеричной системы счисления в двоичную и наоборот
переводится по Триадам.
|
Двоичный код |
Восьмеричная цифра |
Десятичный эквивалент |
|
000 |
0 |
0 |
|
001 |
1 |
1 |
|
010 |
2 |
2 |
|
011 |
3 |
3 |
|
100 |
4 |
4 |
|
101 |
5 |
5 |
|
110 |
6 |
6 |
|
111 |
7 |
7 |
Правило 4.
Перевод чисел из шестнадцатеричной системы счисления в двоичную и наоборот
переводится по тетрадам. Пример, 23E16
= 0010 0011 11012
Далее представлены примеры
перевода целых чисел из одной системы счисления в другую.
Двоичная система счисления:
1100112=
1*20+1*21+0*22+0*23+1*24+1*25
= 5110
11012=
1*23 + 1*22+0*21+ 1*20 =
1310
|
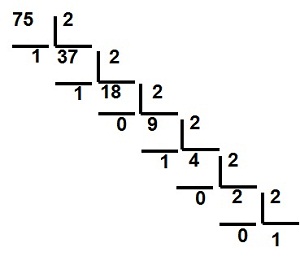 |
7510
= 1 001 0112
|
Восьмеричная система счисления:
3418
=3*82+ 4*81 +1*80 = 22510
10768
= 1*83+0*82+7*81+6*80
= 57410
10768 = 001 000 111 1102
(перевод по триадам)
|
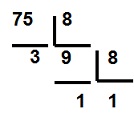 |
7510
= 1138 |
Шестнадцатеричная система:
A1F16
= A*162
+ 1*161 + F*160
= 259110
23Е16 = 2*162+3*161+
Е*160
= 57410
23E16 =
0010 0011 11012
(перевод по тетрадам)
|
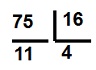 |
7510
= 4B16 |
Перевод дробных чисел из
одной системы счисления в другую
Как правило, это происходит
через промежуточный перевод в десятичную систему:
O,Yp → O,Y10; O,Y10 → O,Yq.
Шаг 1
O,Yp → O,Y10
Если основание СС –
p,
простая дробь содержит
n
цифр и
bk
– цифры дроби (1 ≤
k
≤ n,
0 ≤ bk
≤ p-1),
то она может быть представлена в виде суммы:
O,Yp
= ∑ bk
p-k
Пример: 0,0112 =0*2-1+1*2-2+1*2-3=0,37510
Шаг 2
O,Y10 → O,Yq
1.
Умножить исходную дробь в десятичной СС на p, выделить целую часть – она
будет первой цифрой новой дроби, отбросить дробную часть;
2.
Для оставшейся дробной части операцию умножения с выделением целой и
дробной частей повторять, пока в дробной части не останется 0, или не будет
достигнута желаемая точность. Появляющиеся при этом целые будут цифрами новой
дроби;
3.
Записать дробь в виде последовательности цифр после ноля с разделителем в
порядке их появления в п.1 и 2.
Пример:
0,37510→
O,Y2
0, 375*2 = 0, 750
0, 75*2 = 1, 50
0, 5*2 = 1 , 0
0,37510 = 0,0112
Формы представления чисел
-
С фиксированной
точкой (естественная форма).
-
С плавающей точкой
(нормализованный вид).
С фиксированной точкой
все числа изображаются в виде последовательности цифр с постоянным для всех
чисел положением запятой, отделяющей целую часть от дробной. Например, 0,25;
-10,44; +0,9781.
Число Х10 называется
нормализованным, если оно представлено в виде Х10 =±М10*10±К
, где М10 – мантисса, 0,1≤ М10< 1, К-порядок, целое
положительно десятичное число.
Например: -123410=
-0,1234*104, 0,003=0,3*10-2
При нормализации выполняется
деление числа на 4 составляющих: знак числа, мантисса, знак порядка, порядок.
Для произвольной системы
счисления Хр =± Мр*P±К
, Р-1 ≤ М< 1.
3.
Порядок выполнения работы
1.
Изучить предлагаемый теоретический
материал.
2.
Выполнить следующие
задания:
1.
Запишите первые 20 целых чисел в троичной и
пятеричной системах счисления.
2.
Какие целые числа следуют за числами:
а) 12;
е) 18; л) F16;
б) 1012; ж)
78; м) 1F16;
в) 1112;
з) 378; н) FF16;
г) 11112; и)
1778; о) 9AF916;
д) 1010112; к)
77778; п) CDEF16
3.
Найдите минимальное основание системы
счисления, если в ней записаны все следующие числа 432, 120, 111, 2331.
4.
Какое из чисел больше: 510 или 58,
11112 или 11118?
5.
Какое наибольшее десятичное число можно
записать тремя цифрами:
а) в двоичной системе;
б) в восьмеричной системе;
в) в шестнадцатеричной системе?
6.
Расположите следующие числа в порядке
возрастания: 748, 1100102,
7010, 3816;
7.
Определите максимальное и минимальное из
чисел: 1324;1325; 1326; 1327.
8.
В какой системе счисления 21 + 24 = 100?
9.
В саду 100x
фруктовых деревьев, из которых 33х - яблони, 22х - груши,
16х - сливы, 17х - вишни.
X-?
10.
150510 = X16.
X-?
11.
2CA16 = X2.
X-?
12.
Какое максимальное число можно записать в
двоичной системе счисления пятью цифрами.
13.
Какое наибольшее десятичное число можно
записать тремя цифрами в девятиричной системе счисления?
14.
Расположите следующие числа в порядке
возрастания: 6E16, 1428,
11010012, 10010;
15.
Нормализовать:
0,000011012,
A1,F16.
16.
0,187510=X2,
0,187510=Y8,
0,187510=Z16
17.
5,3(3)10 =
X3.
X-?
18.
Десятичное число 59 эквивалентно числу 214
в некоторой другой системе счисления. Найдите основание этой системы.
19.
В каких системах счисления выполнены
следующие сложения? Найдите основания каждой системы:
а) 98+89=121;
б) 1345 + 2178 = 3523;
в) 10101 + 1111 + 1011
= 20000;
г) 765 + 576 + 677 =
2462;
д) 98 + 56 + 79 = 167.
20.
Сложите числа, а затем проверьте
результаты, выполнив соответствующие десятичные сложения:
|
а) 10111012
и 11101112; |
д) 378 и 758; |
и) A16 и F16; |
|
б) 1011,1012
и 101,0112; |
е) 1658 и 378; |
к) 1916
и C16. |
|
в) 10112, 112
и 111,12; |
ж) 7,58 и
14,68; |
|
|
г) 10112 ,
11,12 и 1112; |
з) 68, 178
и 78; |
|
21.
Вычтите:
|
а) 1112 из
101002; |
д) 158 из 208; |
и) 1А16 из
3116; |
|
б) 10,112 из
100,12; |
е) 478 из
1028; |
к) F9E16 из
2А3016; |
|
в) 111,12 из
100102; |
ж) 56,78 из
1018; |
л) D,116 из
B,9216; |
|
г) 100012 из
1110,112; |
з) 16,548 из
30,018; |
м) ABC16 из
567816. |
22.
Вычислите значения выражений:
а) 2568 + 10110,12
. (608 + 1210) - 1F16;
б) 1AD16 - 1001011002
: 10102 + 2178;
в) 10112
. 11002 : 148 + (1000002 - 408).
23.
Найдите те подстановки десятичных цифр
вместо букв, которые делают правильными выписанные результаты (разные цифры
замещаются разными буквами):
а) ABCDA + FLCDA = FLCLMN;
б) ABCD + EFBCA = GHGCIJ;
в) ABCD + ABCEF = EGDHIG.
4.
Содержание отчета
В отчете следует указать:
-
Цель работы
-
Введение
-
Программно-аппаратные средства, используемые при выполнении работы.
-
Основную часть (описание самой работы), выполненную согласно требованиям к
результатам выполнения лабораторного практикума.
-
Заключение (выводы).
-
Список используемой литературы.
5.
Литература
1.
Могилев А.В., Пак Н.И., Хенкер Е.К.
Информатика. Учебное пособие. – М.: Академия, 2004, 3-е издание.
2.
Могилев А.В., Пак Н.И., Хенкер Е.К.
Практикум по информатике. - М.: Академия, 2005, 2-е изд.
3.
Шауцукова Л.З. Информатика
http://book.kbsu.ru,
2002.
4.
Сырецкий Г.А. Информатика. Фундаментальный курс.
В 2
томах. – БХВ-Петербург,
2007.
5.
Каймин В.А. Информатика. – М.: Инфра-М.
2001, 2-е изд., доп. и перераб.
6.
Острейковский В.А., Полякова И.В.
Информатика. Теория и практика. – М.: Оникс, 2008.
7.
Степанов А.Н. Информатика. Учебник для
вузов. – СПб.: Питер, 2006, 4-е изд.
8.
Рыжиков Ю.И.
Информатика. Лекции и практикум. – СПб.: Корона принт.
2000.
9.
Андреева Е., Фалина И. Информатика. Системы
счисления и компьютерная арифметика. – М.: Лаборатория Базовых Знаний. 1999.
10. Л.З.
Информатика
http://book.kbsu.ru,
2002.
11. В.М.
Введение в информатику http://www.intuit.ru/department/informatics/intinfo,
2006.
12. В.М.
Введение в информатику. Практикум http://www.intuit.ru/department/informatics/intinfopr,
2008.
13. Е.А.
Практическая информатика http://www.intuit.ru/department/se/pinform, 2006
14. Н.Н.
Стили и методы программирования http://www.intuit.ru/department/se/progstyles,
2005
|
